Surface Area Calculator Dekho – Full Explanation

Surface Area Calculator Dekho: Children, whenever we look at any 3D object – whether it’s a ball, a box, or a water tank – we only see and touch its outer surface. The area of this outer part is called the Surface Area. Finding the Surface Area helps us in many tasks, like painting a wall, covering a tank with a sheet, wrapping toys, or preparing the packaging of an object.

Surface Area Calculator Dekho is a digital tool that quickly and easily calculates the area of different 3D shapes. Even if you don’t remember the formulas, you can just enter the values and get the answer instantly.

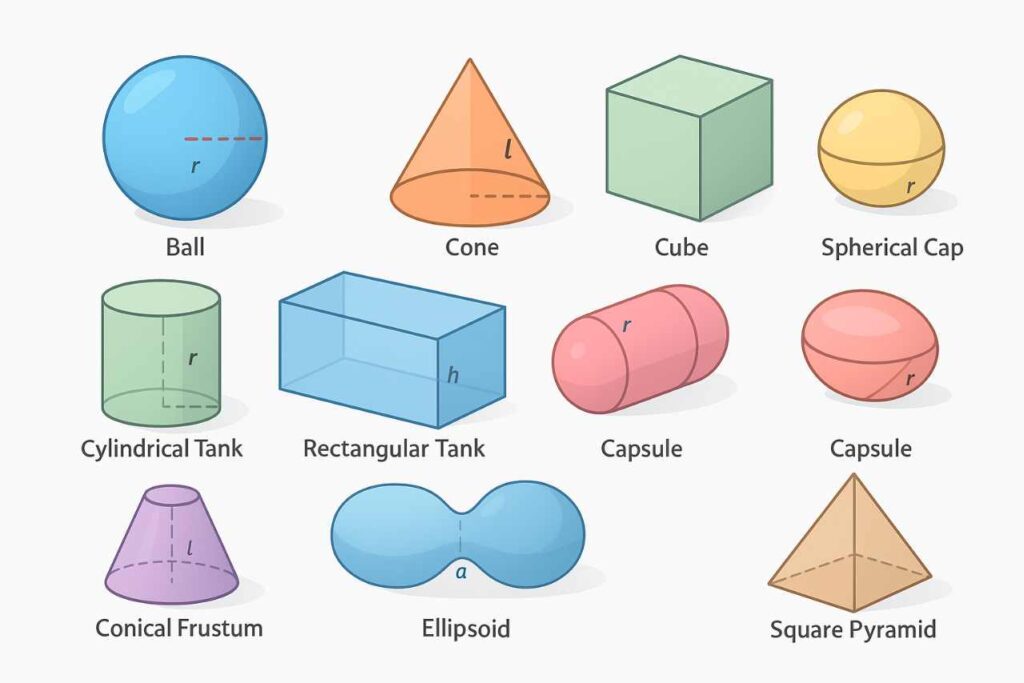
In today’s class we will learn step by step how to calculate the surface area of: Ball, Cone, Cube, Cylindrical Tank, Rectangular Tank, Capsule, Spherical Cap, Conical Frustum, Ellipsoid, and Square Pyramid.

Ball (Sphere) Surface Area Dekho

A ball or sphere is a 3D object whose entire surface is round. Its surface area tells us how much space is on the whole surface of the ball. In real life, this calculation is used for things like footballs, cricket balls, planets, or balloons.

This means that to cover the whole surface of that ball, we would need about 615 cm² of area. If you want to paint it or put a cover on it, this value will be useful for you.

Cone Surface Area Calculator Dekho

A cone is a solid shape whose base is a circle and which has a pointed tip at the top. Ice cream cones, party caps, and traffic cones are practical examples of it. While calculating the surface area of a cone, we need to add both the base and the slant surface.

Cube Surface Area

A cube is a shape whose all sides are equal. Dice, Rubik’s Cube, or small cartons are good examples of a cube. The surface of a cube is made up of 6 equal square faces.

Formula:

This means that to paint or cover the entire surface of the cube, we would need 96 cm² of area. Calculating the surface area of a cube is very useful in packaging industries and in designing building blocks.

Cylindrical Tank Surface Area

A cylinder is a 3D shape whose two bases are parallel circles and which has a height in between. Cylindrical tanks are very common in real life – like water tanks, LPG cylinders, and oil drums.

To calculate the surface area of a cylinder, we need to add both circular bases and the curved surface in between.

Rectangular Tank Surface Area

You can think of a rectangular tank like a large box, whose length, breadth, and height can be different. This shape is often seen in water tanks, swimming pools, and storage containers.

To calculate the surface area of a rectangular tank, we need to add the area of all 6 faces.

Capsule Surface Area

A capsule shape is made up of two hemispheres and a cylinder in between. You can see it in medicine capsules, submarines, or spacecraft modules. This shape is very important in engineering and medical fields because of its curved form.

To calculate the surface area of a capsule, we add the curved area of the cylinder and the areas of the two hemispheres.

Spherical Cap Surface Area Dekho

A spherical cap is the part of a sphere that has been cut off by a plane.

In simple terms: if you cut a ball with a horizontal plane, the top part is called the spherical cap.

This concept is often used in engineering, architecture, tank design, and astronomy.

Conical Frustum Surface Area

A conical frustum is a cone whose top part has been cut off, meaning it is a truncated cone with two parallel circular faces.

In simple terms: if you cut a cone horizontally and remove the small top part, the remaining bottom part is called the conical frustum.

This concept is often used in engineering, tank design, funnel design, and architecture.

Ellipsoid Surface Area (approx.)

An ellipsoid is a 3D shape that is a generalized version of a sphere.

• In a sphere, all three axes are equal.
• In an ellipsoid, the three axes can be different
  • aaa = semi-major axis
  • bbb = semi-minor axis
  • ccc = third axis

Example: The shape of the Earth is approximately an ellipsoid.

The exact surface area of an ellipsoid comes from a complex formula, so an approximation formula is often used.

Square Pyramid Surface Area

A square pyramid is a 3D shape in which:

• Base = Square
• Four triangular faces connect base corners to the apex

In simple terms: if you place a square as the base and draw lines from the corners to the apex at the top, you get a square pyramid.

The surface area and volume of a square pyramid are very useful in geometry, architecture, and packaging design.

Complete Guide to Surface Area of 3D Shapes (Ball, Cone, Cube, Cylinder, Capsule, etc.) in Hindi

In our everyday world, 3D shapes are everywhere. Whether in the packaging industry, tank design, building construction, or school exams, calculating surface area and volume is important everywhere.

In this article, we will look step by step at how to calculate Ball Surface Area, Cone Surface Area, Cube Surface Area, Cylindrical Tank Surface Area, Rectangular Tank Surface Area, Capsule Surface Area, Spherical Cap Surface Area, Conical Frustum Surface Area, Ellipsoid Surface Area (approx.), and Square Pyramid Surface Area.

Tips for Students

1. Always draw the 3D shape before calculation.
2. Separate lateral and base areas.
3. Keep units consistent.
4. Use online calculators for verification: Ball Surface Area, Cone Surface Area, Cube Surface Area, etc.
5. Step-by-step understanding helps exams and practical projects।

Surface Area & Volume Formulas Table

Shape	Surface Area (A)	Volume (V)
Ball / Sphere	\(A = 4 \pi r^2\)	\(V = \frac{4}{3} \pi r^3\)
Cone	\(A = \pi r (r + l), \quad l = \sqrt{r^2 + h^2}\)	\(V = \frac{1}{3} \pi r^2 h\)
Cube	\(A = 6 a^2\)	\(V = a^3\)
Cylindrical Tank	\(A = 2 \pi r (r + h)\)	\(V = \pi r^2 h\)
Rectangular Tank	\(A = 2(lb + bh + hl)\)	\(V = l \cdot b \cdot h\)
Capsule	\(A = 2 \pi r (2r + h)\)	\(V = \pi r^2 \left(\frac{4}{3} r + h\right)\)
Spherical Cap	\(A = 2 \pi R h + \pi r^2\)	\(V = \frac{1}{3} \pi h^2 (3R – h)\)
Conical Frustum	\(A = \pi(r_1 + r_2) l + \pi r_1^2 + \pi r_2^2, \quad l = \sqrt{(r_1 – r_2)^2 + h^2}\)	\(V = \frac{1}{3} \pi h (r_1^2 + r_1 r_2 + r_2^2)\)
Ellipsoid (Approx.)	\(A \approx 4 \pi \left( \frac{(ab)^p + (ac)^p + (bc)^p}{3} \right)^{1/p}, \quad p \approx 1.6075\)	\(V = \frac{4}{3} \pi a b c\)
Square Pyramid	\(A = a^2 + 2 a l, \quad l = \sqrt{(a/2)^2 + h^2}\)	\(V = \frac{1}{3} a^2 h\)

FAQs: Surface Area Calculator Dekho